We study a mathematical model that describes how a “good” bacterial biofilm controls the growth of a harmful pathogenic bacterial biofilm. The underlying mechanism is a modification of the local protonated acid concentration, which in turn decreases the local pH and, thus, makes growth conditions for the pathogens less favorable, while the control-agent itself is more tolerant to these changes. This system is described by a system of 5 density-dependent diffusion-reaction equations that show two nonlinear diffusion effects: porous medium degeneracy and fast diffusion. This is a multi-species expansion of a previously studied single species biofilm model. In this paper we prove the existence of solutions to this model and show in numerical simulations the effectiveness of the control mechanism.
By: Dr Hassan Khassehkhan
This paper, published in the Discrete and Continuous Dynamical Systems Series B (Volume 12, Number 2, September 2009), presents a mathematical model for an amensalistic biofilm control system where a "probiotic" bacterial biofilm controls the growth of a pathogenic bacterial biofilm through the production of protonated lactic acids, which lower the local pH and create unfavorable conditions for the pathogens. Authored by Hassan Khassehkhan, Messoud A. Efendiev, and Hermann J. Eberl, the study extends a single-species biofilm model into a mixed-culture framework, incorporating five dependent variables: protonated lactic acid concentration (C), hydrogen ion concentration (P), pathogen volume fraction (N₁), probiotic volume fraction (N₂), and inert biomass volume fraction (Y).
The model is a quasilinear diffusion-reaction system featuring two nonlinear diffusion effects: porous medium degeneration and fast diffusion. The governing equations describe the dynamics of these variables in a bounded domain, with Dirichlet boundary conditions for microbial flocs or Neumann conditions for biofilms on a substratum. The reaction terms, based on prior work, model the production of protonated acids and hydrogen ions, with biomass growth controlled by piecewise linear functions dependent on C and P.
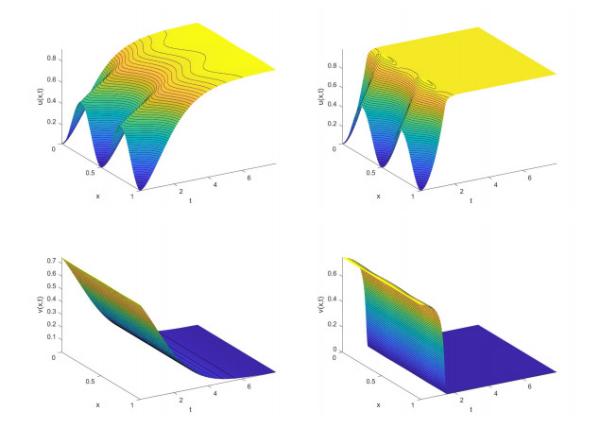
The authors provide the first existence proof for solutions in this mixed-culture biofilm model, addressing the challenges posed by the degenerate diffusion effects, which prevent the straightforward application of standard analytical techniques. Numerical simulations illustrate the model’s behavior, showing two scenarios: limitation and eradication of pathogens. In the eradication scenario, simulations demonstrate that pathogens are inactivated first in deeper biofilm layers due to higher acid concentrations, contrasting with antibiotic treatments where outer layers are affected first. The simulations also highlight the merging of initially separated colonies into multi-species structures, with probiotics eventually dominating due to their greater tolerance to growth limiters.
The study concludes with insights into the amensalistic control mechanism, supported by numerical results, and notes the absence of a uniqueness result for solutions, posing a question for future research. The work is supported by funding from the Canada Research Chairs Program, NSERC, and computational resources from SHARCNET.
Background and Motivation
Biofilms are microbial communities that adhere to surfaces and are embedded in a protective extracellular matrix. They are notoriously resistant to antibiotics and other treatments due to limited penetration of substances and the protective biofilm structure. Traditional methods for biofilm control often fail, particularly against pathogenic bacteria in medical and food industry settings.
To address this, researchers explore a biocontrol strategy using probiotic bacteria that indirectly suppress pathogens by modifying their environment. This form of microbial interaction is called amensalism, where one species is inhibited while the other is unaffected or benefits. The model extends previous work by including both species in the biofilm (a mixed-culture system), making it more realistic and complex.
Mathematical Model
The model consists of a system of five nonlinear partial differential equations (PDEs) with degenerate and fast diffusion terms, describing:
Concentration of protonated lactic acid (C)
Concentration of hydrogen ions (P), related to pH
Volume fraction of pathogenic biomass (N₁)
Volume fraction of probiotic biomass (N₂)
Volume fraction of inert (dead) biomass (Y)
The model incorporates two nonlinear diffusion mechanisms:
Porous medium degeneracy: slows diffusion in low-density regions.
Fast diffusion: ensures bounded growth in high-density regions.
The system accounts for both spatial diffusion and reaction kinetics (growth, inhibition, and inactivation of biomass), with parameters estimated from experimental data.
Existence of Solutions
One of the key contributions of this paper is the proof of existence of weak solutions to the system of equations under suitable boundary and initial conditions. The authors rigorously show, using regularization and compactness arguments, that solutions exist in the distributional sense. However, uniqueness of solutions is not established, which remains an open mathematical question.
Numerical Simulations
To validate and explore the behavior of the model, the authors conduct numerical simulations using finite difference methods on a two-dimensional grid. They implement a semi-implicit time discretization scheme optimized for high-performance computing environments.
Two scenarios are simulated:
Pathogen Growth Limitation (Parameter Set I):The probiotic slows down but does not eradicate the pathogen. The pathogen persists in inner layers, while probiotics expand at the biofilm edges.
Pathogen Eradication (Parameter Set II):Modified parameters allow the probiotic to completely outcompete and eventually inactivate the pathogen, leading to accumulation of inert biomass. The simulation shows the biofilm growing thicker and the pathogen being eliminated, especially from deeper layers near the surface.
A key insight is that, unlike antibiotic treatments, which typically affect the outer biofilm layers, this biocontrol strategy leads to pathogen inactivation from the inner regions outward-a reversal of the conventional treatment outcome.
Conclusion
This study contributes both theoretically and practically:
It presents a robust mathematical framework for modeling dual-species biofilms under amensalistic interaction.
It proves the existence of solutions for this highly nonlinear and degenerate system.
It provides simulations demonstrating how probiotics can effectively control or eradicate pathogenic biofilms through environmental modification rather than direct competition.
These findings have implications for medical and food safety applications where biofilms are a persistent problem. Future work will address convective transport in the surrounding liquid and seek uniqueness results for the proposed system.
Download the article to read:
 | A Degenerate Diffusion-Reaction Model of an Amensalistic Biofilm Control System: Existence and Simulation of Solutions |

